грузки

Л1 = 0; Л2 = 0; S = q(ab/2f), т.е. нормальные усилия вдоль осей Ох и Оу равны нулю по всей поверхности, а сдвигающие силы всюду постоянны.

Главные напряжения также по всей оболочке постоянны, направлены под углом 45° к координатным осям и равны вдоль выпуклых вниз парабол Nrii=q(a,b/2f), а вдоль выпуклых вверх парабол

Лпл -g(ab/2f).

Таким образом, выпуклая поверхность всюду сжата постоянной силой, а вогнутая растянута той же силой.

Прямолинейные бортовые элементы безмоментны; они воспринимают сдвигающие усилия от оболочки. Нормальное усилие в бортовом элементе нарастает по линейному закону от нуля до М=51о у опоры.

3.4.4. Цилиндрические оболочки и складки

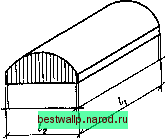
Элементами цилиндрической оболочки являются: собственно оболочка, бортовой продольный элемент, опорные и промежуточные диафрагмы (рис. 3.16).

Цилиндрические оболочки в зависимости от соотиощения размеров делятся на длинные при Ulkl и короткие при IJkKl-

В ряде случаев цилиндрические оболочки могут рассчитываться как балки или тонкостенные стержни с недеформируемым поперечным контуром.

Цилиндрические оболочки разделяют на два основных класса: оболочки симметричного сечения при соотнощении hlhS при симметричных загружениях, а также при односторонних загруженнях, составляющих не более Д интенсивности полного симметричного загружеиия, причем односторонняя нагрузка при расчете должна быть заменена полной той же интенсивиости; оболочки с соотноще-иием /i 2>l прн наличии не менее трех поперечных ребер.

Для неразрезных оболочек вместо U в расчете принимается 1р - расстояние между нулевыми точками эпюры моментов.

Для приближенного определения поперечных моментов рассматривается полоса единичной ширины, вырезанная двумя поперечными сечениями в центре пролета оболочки. К вырезанному элементу при кладываются разность сдвигающих усилий, действуюЩих в плоскостях срезов, и внешние нагрузки. От этих воздействий в поперечных сечениях полосы определяются изгибающие моменты и нормальные силы. Поперечный нзгиб принимается меняющимся вдоль главного пролета по тому же закону, что и прогиб.

3.4.5. Круглые мембраны

Мембраны, работающие в упругой стадии. Мембрана, очерченная по поверхности вращения, может быть рассчитана по формулам безмоментной теория оболочек при условии, что все усилия, возникающие в ней, растягивающие, а деформация от загружения меняет кривизну не более чем на 10 % (геометрически линейная задача).

Плоская мембрана, загруженная равномерно распределенной нагрузкой, может быть рассчитана по формулам:

: = 0,662 V ga/Eh; Лг=о = 0,423 V Eq а? h)

Л?г=а = 0,328у Eqaih

(формулы применимы при Nr=o/hR),

где W - прогиб; а -- радиус мембраны; R - расчетное сопротивление материала мембраны; h - толщина мембраны.

Мембраны, работающие в пластической стадии. Полиостью пластическая мембрана имеет в любой точке по любому направлению усилие ah=T. Для такой мембраны уравнение изогнутой поверхности

W = riq/4G.rh,

где г - переменный радиус.

Условие применимости формулы для стали СтЗ

3.4.6. Расчет пологих нитей (рис. 3.17)

Если при фиксированной внешней нагрузке известна ордината хотя бы одной точки С нити, то расчет ее может быть произведен в такой последовательности:

(3.1) (3.2)

Y(x)M{x)/H,

где М - балочный момент; Y(x) - уравнение кривой провисания иити.

Длина нити определяется по формуле

Q2 (х) dx,

(3.3)

где Q - балочная поперечная сила.

При догружении дополнительной нагрузкой распор может быть определен из кубического уравнения

EF 21Н1

Qldx~H

EF 21

Qldx=0, (3.4)

где Hi - распор после догружения; Но - распор до догружения; Qi - балочная поперечная сила после догружения; Qo - то же, до догружения.

Уравнение (3.4) учитывает упругое удлинение иити при догружении (табл. 3.15).